Using moving average filters for hard filtering.
It’s September, most of you will come back to work, others don’t remember what is that of holidays, and others, luckiest people, will start your holidays soon. I am in the first group, so I have to back to work, and also, back to write here :).
Ok, we are on out first day at work after holidays, and the boss come to our table and tell as about an strange undesirable harmonic on a very important signal, and ask you to attenuate this harmonic with the lowest delay you can reach. If you want to attenuate only one harmonic, the only option you have is a notch filter with high Q factor, this way you can almost eliminate the harmonic, but this kind of filters, when they are implemented on digital systems, have one problem. Notch filters are in the group of resonant filters, so exists the possibility that, with certain input signals, our filter will be unstable. And remember!, you don’t have time to calculate the coefficients, implement the filter, and test it with all possible input signals for ensure it is stable.
At this point, where you don’t have enough time, or simply you feel lazy after holidays, you need some filter to reject a certain harmonic, and FIR filters can save you. If you remember the frequency response of FIR filter, it has a series of notch that depend of the filter order, and the value of its coefficients, so we can calculate all coefficients with some Matlab or Octave script and we will have a high attenuation on desired harmonics, but remember!, yesterday you was at the beach, and for you, now, to compute the fir coefficients to adjust the notch to the desired frequency is like reach the top of Montblanc, so, you have to find some easily way to reject this infernal harmonic.
What do you think about the complexity of the next equation?
\[f_{NOTCH} = \frac{fs}{n}\]Is true that is a little bit more complex than a addition, but is easy anyway. This equation is corresponding with the frequency of the first notch when we use a simple moving average filter.
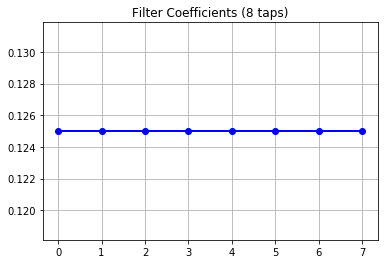
A moving average filter has a similar response than FIR filters, and, in fact, a moving average filter is a FIR filter, where all coefficients have a value of 1/n, so the impulse response will be an horizontal line. Next figure show the impulse response, that isn’t more that the coefficients, for a 8th order moving average filter.
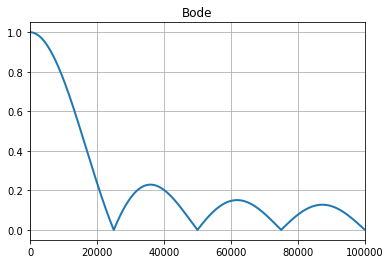
With this coefficients, I’ve designed a filter with a sampling frequency of 200kHz, and the frequency response of this filter is showed on the next figure.
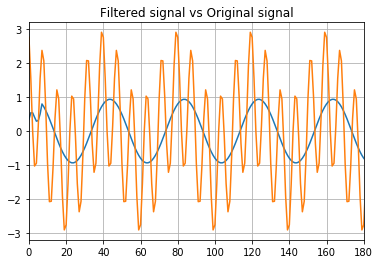
As we had calculate, for 8th order filter, with a fs of 200kHz, the first notch is located at 200e3/8=25e3. Now I’ve created a sample signal of 5kHz, and a high harmonic of 25kHz, and, as you can see, the 25kHz harmonic has rejected at all.
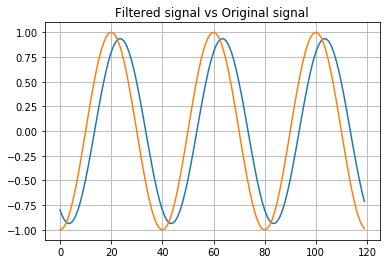
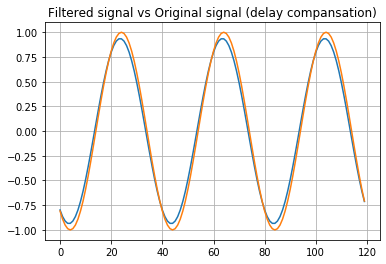
The next figure show the first harmonic of the signal, vs the signal filtered. You will see a delay between 2 signals. That delay is corresponding almost at all due to the pipeline delay, and this delay is known as group delay.
Group delay is well known, and its value is defined as n/2 samples, so, depends exclusively of the FIR order. If we compensate this delay, the resulting signal will show us the real delay between signals.
Also, you can see a little attenuation on 5kHz signal, that’s because 5kHz is out of the 0dB band attenuation, due to this kind of filter, the pass band is narrow, and depends of the filter order.
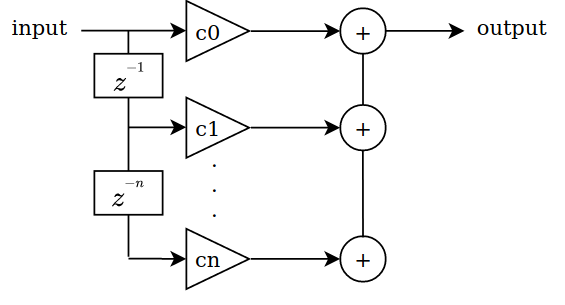
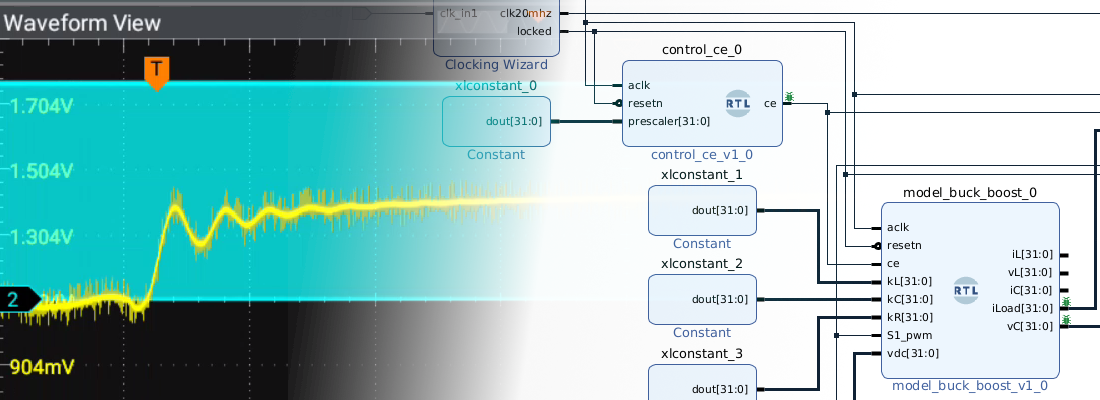
Now, let’s talk about the implementation on FPGA. As I said, the reason to use this kind of filters is how easy is compute a narrow reject band filter, but the implementation is the second big advantage of this filter. Next figure shows the diagram of a FIR filter.
Moving average filters are a specific configuration of these filters, where all coefficients have the same value, 1/n. If we define n as a power of 2, multiplications will be transformed on shifts, so the implementation of this filter will be reduces to adders and shifts, which reduce at the minimum the logic used.
/**
Module name: mv_avg_filter_8_v1_0
Author: P Trujillo ([email protected])
Date: Aug 2020
Description: 8th order moving average filter
Revision: 1.0 Module created.
**/
module mv_avg_filter_8_v1_0 (
input clk,
input rst,
input [31:0] i32_prescaler,
input signed [13:0] is14_data,
output signed [13:0] os14_data
);
reg [31:0] r32_prescaler_counter; /* Counter for prescaler */
reg signed [14:0] rs14_pipe1; /* Pipeline register */
reg signed [14:0] rs14_pipe2; /* Pipeline register */
reg signed [14:0] rs14_pipe3; /* Pipeline register */
reg signed [14:0] rs14_pipe4; /* Pipeline register */
reg signed [14:0] rs14_pipe5; /* Pipeline register */
reg signed [14:0] rs14_pipe6; /* Pipeline register */
reg signed [14:0] rs14_pipe7; /* Pipeline register */
reg signed [14:0] rs14_pipe8; /* Pipeline register */
always @(posedge clk)
if (rst) begin
rs14_pipe1 <= 14'd0;
rs14_pipe2 <= 14'd0;
rs14_pipe3 <= 14'd0;
rs14_pipe4 <= 14'd0;
rs14_pipe5 <= 14'd0;
rs14_pipe6 <= 14'd0;
rs14_pipe7 <= 14'd0;
rs14_pipe8 <= 14'd0;
r32_prescaler_counter <= 32'd0;
end
else
if (r32_prescaler_counter >= i32_prescaler) begin
rs14_pipe1 <= is14_data;
rs14_pipe2 <= rs14_pipe1;
rs14_pipe3 <= rs14_pipe2;
rs14_pipe4 <= rs14_pipe3;
rs14_pipe5 <= rs14_pipe4;
rs14_pipe6 <= rs14_pipe5;
rs14_pipe7 <= rs14_pipe6;
rs14_pipe8 <= rs14_pipe7;
r32_prescaler_counter <= 0;
end
else
r32_prescaler_counter <= r32_prescaler_counter+32'd1;
assign os14_data = (rs14_pipe1>>>3) + (rs14_pipe2>>>3) + (rs14_pipe3>>>3) + (rs14_pipe4>>>3) +
(rs14_pipe5>>>3) + (rs14_pipe6>>>3) + (rs14_pipe7>>>3) + (rs14_pipe8>>>3);
endmodule
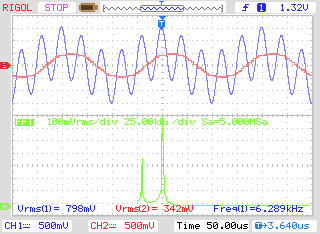
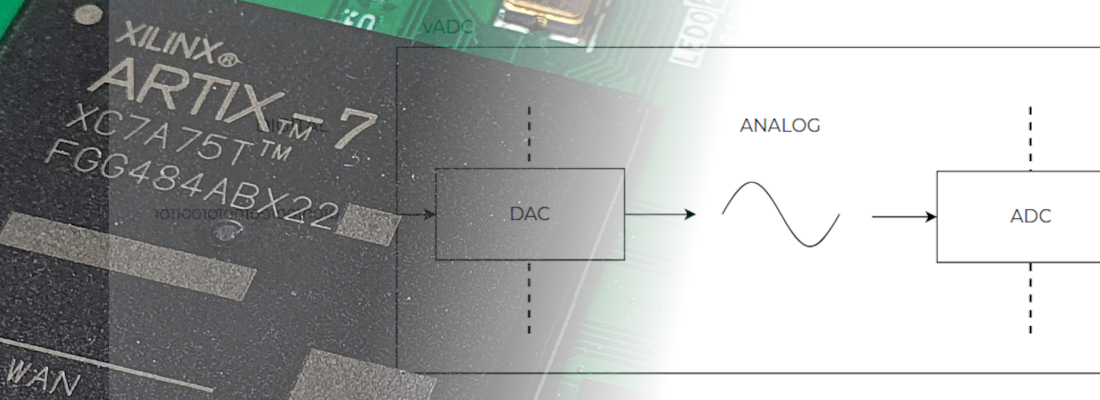
Filter was been tested on Digilent’s Eclypse Z7 with ZMOD DAC and ZMOD ADC, and the result is shown of the next scope capture.
As we can see, all the 25kHz ripple has been rejected, and the output signal only contains the 5kHz harmonic.
For use this filter with other frequencies, we have 2 variables that we can modify, first, the filter order, because as we can see, the frequency of the first notch is related directly with the filter order. Also, remember that filter has infinite number of notches at 2nfnotch, so we can use any of different notch to filter the undesirable frequency, but notice that this filter is a low pass filter, so the attenuation around notches will be greater when we increase the frequency. Also, you have to think that increasing the filter order, group delay will be increased too. The other variable we can modify to adjust the notch frequency is the sampling frequency. In my case, ZMOD ADC acquire at 100MHz, but the filter performs a decimation to set the new sampling frequency. It’s important take care with the aliasing, because if the sampling frequency of the filter is lower than twice of the maximum signal frequency, resulting signal will be distorted. For avoid that, and thinking that the hardware is designed and cannot be modified, you can add a digital low pass filter to attenuate high order harmonics, but in this case, the resulting delay will be increased by the new digital anti-aliasing filter.
With this post I wanted to show you how easy is use this kind of filters and how, in certain cases, they could be a great idea. Thanks for read!