Proportional – Integral regulator. Implementation and verification.
In the last post we talked about digital control loops. In short, we talked about the elements that we can find in digital, or analog, control loops. The first of them is an element to acquire the difference between the actual output of the system, and the desired output, in other words, the error. Also, we will need an element that will be capable to change the output of the system we need to control. This element is named as actuator. Finally, we need an element that computes the control action applied to the actuator, in order to make the error as closest to zero as possible. This last element is known as regulator. In this post we will focus in the regulator, how to implement a regulator using Verilog ans also how we can verify its behavior through simulation.
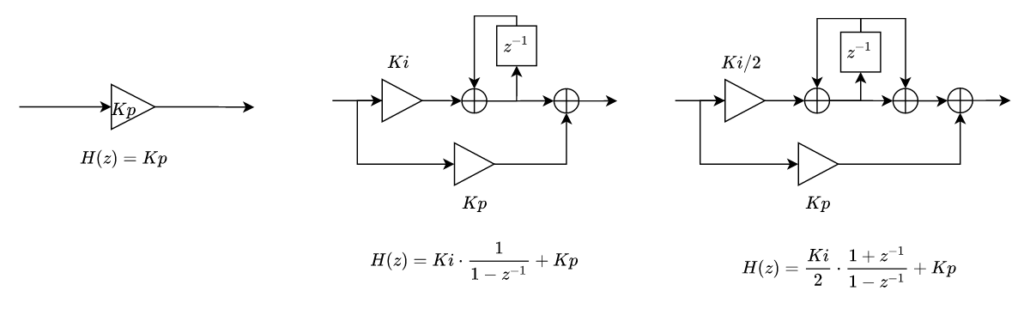
From the last post we know that there are different kind of regulators according the parallel branches that it has. If we only use a branch with a gain, we will obtain a P regulator. On the other side, if we add an integrator to a new branch, we will obtain a PI regulator. The main element of the integral branch is the integrator, and depending the method we use to discretize the term, we can obtain different structures. In the figure below you can find a proportional regulator, a proportional – integral regulator using the impulse invariance method (center), and a proportional – integral regulator using the Tustin method (left).
At this point we already have a model of the regulator, therefore the next will be the implementation in the FPGA. As usual, I will use Verilog to implement the regulator module, however, I will use SystemVerilog to implement the testbench.
First of all we need to define the interfaces. For this kind of modules I like to use AXI Stream interface since its easy to connect them to other modules, and keep the block design clean. Also, we will need 2 additional inputs to set the proportional and the integral gains. The AXI Stream interface will be use for the input, reference and the output, being the last the only master interface. Also, since the regulator has an integrator inside, we need to define the maximum and the minimum output that we will allow. This is very important to avoid overflows. Regarding the widths, we will allow to define different widths for gains and inputs/outputs. This configuration will allow later to send the gains through AXI4 Lite that has a width of 32 bits, while the input and output widths will remain in 16 or whatever be the ADC resolution. Also to improve the resolution inside the module, I have added an internal width. For all the widths defined we need to define the how many of these bits are dedicated to the decimal part. Inside the module, the integer width will be computed. The module declaration will look like the next.
module axis_pi_v1_0 #(
parameter inout_width = 12,
parameter inout_decimal_width = 11,
parameter internal_width = 16,
parameter internal_decimal_width = 15,
parameter gain_width = 12,
parameter gain_decimal_width = 11
)(
input aclk,
input resetn,
input [gain_width-1:0] kp, /* regulator gain */
input [gain_width-1:0] ki, /* regulator gain */
input signed [inout_width-1:0] output_max, /* max saturation level */
input signed [inout_width-1:0] output_min, /* min saturation level */
input [inout_width-1:0] s_axis_input_tdata, /* slave axis input data */
input s_axis_input_tvalid, /* slave axis input tvalid */
output s_axis_input_tready, /* slave axis input tready */
input [inout_width-1:0] s_axis_reference_tdata, /* slave axis reference data */
input s_axis_reference_tvalid, /* slave axis reference tvalid */
output s_axis_reference_tready, /* slave axis reference tready */
output [inout_width-1:0] m_axis_output_tdata, /* master axis output data */
output reg m_axis_output_tvalid, /* master axis output tvalid */
input m_axis_output_tready /* master axis output tready */
);
Then, inside the module, first we need to define as localparam the integer widths. Also, for each input we need to definie the same but changing its original width by the internal widths. Now, we have to resize the inputs of the module (input, reference, and gains), to the internal withs, keeping its value. This is done adding a padding of 0 in the low side, and a padding of the MSb in the high side. Using this method we will keep the sign and the value.
localparam inout_integer_width = inout_width - inout_decimal_width; /* compute integer width */
localparam gain_integer_width = gain_width - gain_decimal_width; /* compute integer width */
localparam internal_integer_width = internal_width - internal_decimal_width; /* compute integer width */
wire signed [internal_width-1:0] input_internal; /* input resized with internal width */
wire signed [internal_width-1:0] reference_internal; /* reference resized with internal width */
wire signed [internal_width-1:0] kp_internal; /* kp resized with internal width */
wire signed [internal_width-1:0] ki_internal; /* ki resized with internal width */
assign input_internal = { {(internal_integer_width-inout_integer_width){s_axis_input_tdata[inout_width-1]}},
s_axis_input_tdata,
{(internal_decimal_width-inout_decimal_width){1'b0}} };
assign reference_internal = { {(internal_integer_width-inout_integer_width){s_axis_reference_tdata[inout_width-1]}},
s_axis_reference_tdata,
{(internal_decimal_width-inout_decimal_width){1'b0}} };
assign kp_internal = { {(internal_integer_width-gain_integer_width){kp[gain_width-1]}},
kp,
{(internal_decimal_width-gain_decimal_width){1'b0}} };
assign ki_internal = { {(internal_integer_width-gain_integer_width){ki[gain_width-1]}},
ki,
{(internal_decimal_width-gain_decimal_width){1'b0}} };
When we have all the inputs resized, we can start to perform mathematical operations. The first one will be compute the error. The formula for the error is very simple, only you have to compute the difference between the reference and the input. Once the error is computed, we can apply the gains to the error. In order to reduce the total delay of the regulator, and always that the timing restrictions allow it, the multiplications will be performed combinationally. In case that you need to add a register in the multiplication, this register is added using one of the registers that the multiplier has included, so no external register will be used.
assign error = $signed({reference_internal[internal_width-1], reference_internal}) - $signed({input_internal[internal_width-1], input_internal});
assign ki_error = error * ki_internal;
assign kp_error = error * kp_internal;
For the proportional part is all done. The value of kp_error is directly the proportional action. Regarding the integral action, at this point we have the gain applied to the error, and now we have to accumulate this value. The implementation of the integrator discretized using the impulse invariance method is very simple, and it can be done using an accumulator with a clock enable. As clock enable we can use the data valid input of the input AXI stream port. the integrator I have implemented is a little bit more complicated since it has included the saturation. let me explain what I have done.
First of all, you can find the clock enable for the integrator, in this case, the signal s_axis_input_tvalid. Then you can find the integrator itself, but it only accumulates when:
- The output before the saturation is LESS than the POSITIVE saturation and is GREATER than the NEGATIVE saturation, OR
- the output before saturation is GREATER than the POSITIVE saturation and the value to accumulate is NEGATIVE, OR
- the output before saturation is LESS than the NEGATIVE saturation and the value to accumulate is POSITIVE
In short, the accumulator only accumulates when the output is between the maximum and the minimum values, and also when it is saturated but the control action is opposite to the saturation.
This kind of saturation stops the accumulation when the output is saturated, so the recovery when the error changes it sign is instantaneously.
/* integral */
always @(posedge aclk)
if (!resetn)
integral_register <= {(internal_width+1){1'b0}};
else
if (s_axis_input_tvalid)
if (($signed(output_nsat > output_min) && $signed(output_nsat < output_max)) ||
((ki_error > 0) && $signed(output_nsat < output_min)) ||
((ki_error < 0) && $signed(output_nsat > output_max)))
integral_register <= integral_register + ki_error;
else
integral_register <= integral_register;
assign control_action_sum = (kp_error >>> internal_decimal_width) + (integral_register >>> internal_decimal_width);
There are other kind of saturation using an anti-windup branch. This method add a subtraction to the integral accumulator that subtract the difference between the real output and the saturated output, keeping the integrator with a low value oscillation.
One we have the proportional action and the integral action, we have to add them. Before to add them we need to make a shift of the decimal widths in order to keep the initial width.
The final step in the regulator is resize the output value from the internal width, to the inout width. This assignement is registered and enabled with the s_axis_input_tvalid signal in order to avoid output changes if this signal is not set. Notice that the proportional branch is combinational, so changes in the input will produce changes in the output with the clock enable signal cleared.
/* output register */
always @(posedge aclk)
if (!resetn)
output_nsat <= {internal_width{1'b0}};
else
if (s_axis_input_tvalid)
output_nsat <= control_action_sum >>> (internal_decimal_width-inout_decimal_width);
assign m_axis_output_tdata = (output_nsat > output_max)? output_max: (output_nsat < output_min)? output_min: output_nsat;
Now we have to think how to verify the behavior of the module. For this task we have several options. The first that I though is to simulate a real application where I connect the output of the regulator to the input of a second order system, then design several tests with different references and check the behavior. Later I can implement the same in MATLAB and compare the output. Something like this was that I did to verify the behavior of the biquad filter in this post. This method is very useful, but this time I have preferred develop all the verification in Verilog, since later, if we need to automatize the verification, we only need python and a synthesis tool like Icarus or Vivado. For the testbench I have used System Verilog since it allows some commands that makes the verification easy.
The testbench contains some functions that I used several times in the code, and also I have developed a mathematical model of the regulator that I will use to compare with the module. The regulator described in the testbench will act as golden code.
The first function in the testbench is check_model. Its purpose in compare the model and the module outputs and send messages to the console indicating if both are equal or not. I have added a definition with the error allowed that is configured in ten. After we will see it purpose. Something interesting of this function is the use of the instructions $info and $error, that shows in console, in addition to the message, the module that called the instruction, and the simulation time. I have comment the $finish instruction because I don’t want that an error stops the simulation. Instead of use the instructions finish, you can use $fatal, however, as I am verifying the verification code, is better for me keep this instructions separated.
function check_model();
begin
if ((m_axis_output_tdata <= (model_output + `error_allowed)) && (m_axis_output_tdata >= (model_output - `error_allowed))) begin
$info("TEST OK: Module output is %0d and expected output is %0d", m_axis_output_tdata, model_output);
end
else begin
$error("TEST FAILED: Module output is %0d and model output is %0d", m_axis_output_tdata, model_output);
// $finish();
end
end
endfunction
The second relevant function is the model itself. I have design 3 different models, each of them with different levels of complexity. The firstone if the less complicated, and only compute the output regardless the saturation.
function compute_model();
begin
model_error = (reference_real - input_real);
model_proportional = model_error * kp_real;
model_integral = model_integral + (model_error * ki_real);
model_output_real = (model_proportional + model_integral) ;
model_output = model_output_real * 2**(inout_decimal_width);
end
endfunction
With this both functions, and some code (you can find all the testbench code in Github), we can execute the test. First of all, I have test the proportional branch, so the test configure the kp with a non-zero value and the ki with a zero value, then set a fixed input and reference levels. What we can see in the console is the next.
INFO: ./axis_pi_tb.sv:238: Testing proportional gain.
Time: 0 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:240: Wait 1us.
Time: 0 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:242: Release module reset
Time: 1000 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:244: Wait 1us.
Time: 1000 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:249: Set kp = 0.01000 and ki = 0.00000
Time: 2000 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:253: Set input = 0.10000 and reference = 0.00000
Time: 2000 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:256: Wait 1 clk cycle.
Time: 2000 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:259: Set data valid signal.
Time: 2010 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:170: TEST OK: Module output is -17 and expected output is -16
Time: 2020 Scope: axis_pi_tb.check_model
The test is executed without any issue. You can see that the output of the model and the module are different. This is due to fact than the model is computed using float variables of 64 bits, while the module uses 16 bits. For the proportional gain the error is not relevant. Lets see what happens with the integral test.
For this test, the conditions are the same, but this time the kp value is set to zero and the ki value is set to a non-zero value.
INFO: ./axis_pi_tb.sv:272: Testing integral gain.
Time: 2020 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:187: Resetting model.
Time: 2020 Scope: axis_pi_tb.reset_model
INFO: ./axis_pi_tb.sv:276: Wait 1us.
Time: 2020 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:278: Release module reset
Time: 3020 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:280: Wait 1us.
Time: 3020 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:285: Set kp = 0.00000 and ki = 0.00100
Time: 4020 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:289: Set input = 0.15000 and reference = 0.00000
Time: 4020 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:292: Wait 1 clk cycle.
Time: 4020 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:295: Set data valid signal.
Time: 4030 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:170: TEST OK: Module output is 0 and expected output is -2
Time: 4050 Scope: axis_pi_tb.check_model
INFO: ./axis_pi_tb.sv:307: Repeat 50 times with same conditions.
Time: 4050 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:170: TEST OK: Module output is -121 and expected output is -125
Time: 4550 Scope: axis_pi_tb.check_model
INFO: ./axis_pi_tb.sv:321: Repeat 500 times with same conditions.
Time: 4550 Scope: axis_pi_tb
ERROR: ./axis_pi_tb.sv:173: TEST FAILED: Module output is -1321 and model output is -1354
Time: 9550 Scope: axis_pi_tb.check_model
For the first execution we can see an error of 2. Notice that the values of the model have a width of 16 bits, with a decimal part of 14 bits, so 2 counts are an error of
\[\frac{2}{2^{14}}=1.22 e-4\]so we can say that the error is negligible. When we execute the algorithm 50 times, the integratos accumulates the input, but not only the input, but also the error, and it is increased to 4. if we continua executing the algorithm, we can see for the 550 repetitions, the error accumulated is 33. if we need to reduce the error we can increase the internal witdhs, and also the gain and inputs widths, since the error is also in the gains quantification.
Next I have test both actions in parallel in order to verify the addition.
INFO: ./axis_pi_tb.sv:355: Testing proportional + integral gain.
Time: 9550 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:187: Resetting model.
Time: 9550 Scope: axis_pi_tb.reset_model
INFO: ./axis_pi_tb.sv:359: Reset module.
Time: 9550 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:361: Wait 1us.
Time: 9550 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:363: Release module reset
Time: 10550 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:365: Wait 1us.
Time: 10550 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:370: Set kp = 0.10000 and ki = 0.00100
Time: 11550 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:374: Set input = 0.00000 and reference = 0.10000
Time: 11550 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:377: Wait 1 clk cycle.
Time: 11550 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:380: Set data valid signal.
Time: 11560 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:170: TEST OK: Module output is 163 and expected output is 165
Time: 11580 Scope: axis_pi_tb.check_model
INFO: ./axis_pi_tb.sv:392: Repeat 50 times with same conditions.
Time: 11580 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:170: TEST OK: Module output is 242 and expected output is 247
Time: 12080 Scope: axis_pi_tb.check_model
Once both branches are verified, we have to verify the saturation. For this test I have designed a new regulator model, this time adding the saturation expected behavior. The model is the next.
function compute_model_sat();
begin
model_error = (reference_real - input_real);
model_proportional = model_error * kp_real;
ki_gain = ((reference_real - input_real) * ki_real);
if (((model_output_nsat < output_max_real) && (model_output_nsat > output_min_real))
|| ((model_output_nsat > output_max_real) && (ki_gain < 0))
|| ((model_output_nsat < output_min_real) && (ki_gain > 0)))
model_integral = model_integral + (model_error * ki_real);
else
model_integral = model_integral;
model_output_nsat = (model_proportional + model_integral);
if (model_output_nsat > output_max_real)
model_output_real = output_max_real;
else if (model_output_nsat < output_min_real)
model_output_real = output_min_real;
else
model_output_real = model_output_nsat;
model_output = model_output_real * 2**(inout_decimal_width);
end
endfunction
Executing the test for this model, and increasing the value of the constants in order to achieve the saturation in less time, the output of the console is the next.
INFO: ./axis_pi_tb.sv:408: Testing saturation.
Time: 12080 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:187: Resetting model.
Time: 12080 Scope: axis_pi_tb.reset_model
INFO: ./axis_pi_tb.sv:412: Reset module.
Time: 12080 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:414: Wait 1us.
Time: 12080 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:416: Release module reset
Time: 13080 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:418: Wait 1us.
Time: 13080 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:423: Set kp = 0.80000 and ki = 0.01000
Time: 14080 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:425: Test positive saturation
Time: 14080 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:428: Set input = 0.00000 and reference = 1.00000
Time: 14080 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:432: Set positive saturation = 1.90000 and negative saturation = -1.90000
Time: 14080 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:436: Repeat 300 times with same conditions.
Time: 14080 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:170: TEST OK: Module output is 31130 and expected output is 31130
Time: 17080 Scope: axis_pi_tb.check_model
INFO: ./axis_pi_tb.sv:450: Test negative saturation
Time: 17080 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:453: Set input = 0.00000 and reference = -1.00000
Time: 17080 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:457: Repeat 300 times with same conditions.
Time: 17080 Scope: axis_pi_tb
INFO: ./axis_pi_tb.sv:170: TEST OK: Module output is -31130 and expected output is -31130
Time: 20080 Scope: axis_pi_tb.check_model
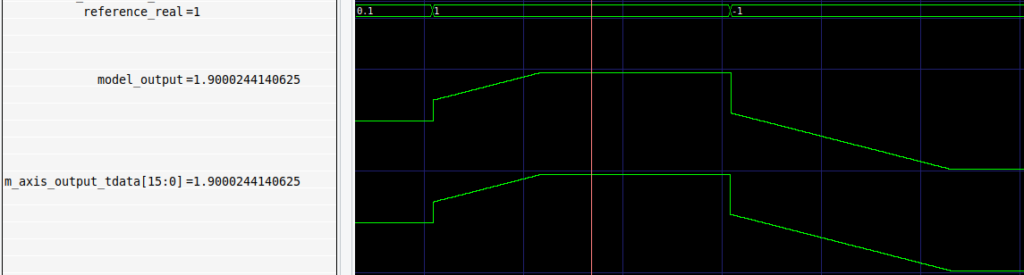
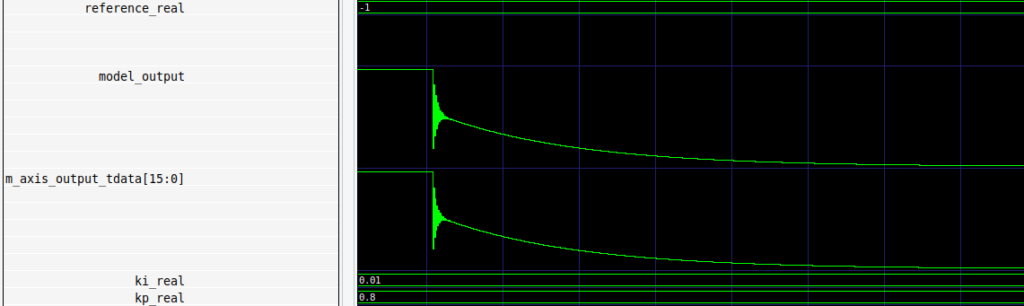
The console indicates than both the module and the model reach the saturation. For this test is more interesting to check the behavior using a waveform viewer. In the next figure we can see the model output and the value of the output of the module. Both signals are escalated in order to see the real value. We can see how, when the reference is 1, both outputs increases until reach the positive saturation, then when the reference changes to -1, we can see the first step produced by the proportional action, and then the integral action starts to integrate at the same time, This indicates than the integrator is freeze and, after a reference changes, the integral actions starts to integrate to the new reference.
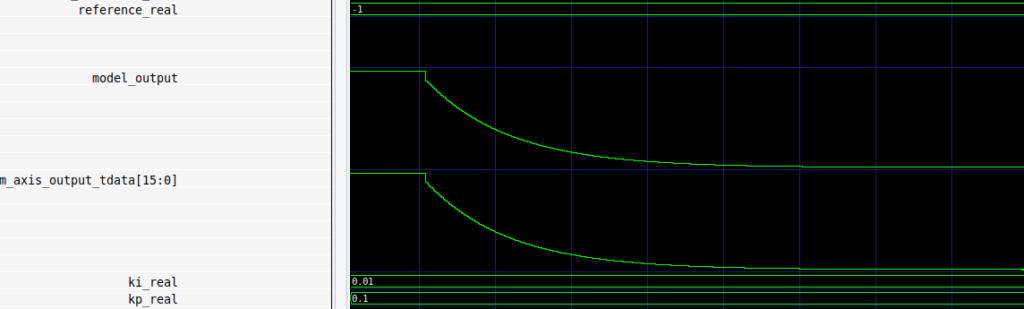
With these tests we have verify both proportional and integral branch, the output adder, the error compute and the saturation. To complete the testbench, I have designed one test where the input and the output of the regulator are connected, in order to perform a loopback test. For a kp of 0.1 and ki of 0.01, and a reference of -1 the result is the next.
If we increase the value of the kp to 0.8, we can see how the output oscillates in the first step.
Experiment with regulators and systems is been very (very very…) interesting. For my job, I have to design and implement regulators and also verify its behavior and match the module that I have designed in verilog with other models designed in MATLAB or any other tool, and the moment when the response of your module is the same (regardless the quantification error), is very exiting. The same happens with filters designed in MATLAB or Python, and then implemented in Verilog.
Regarding the verification, there are many opensource tools like cocotb or Verilator that you can use to write and execute your tests. The way what you design your text is completely up to you. If you are comfortable with Python, you can use cocotb, on the other hand if you like C, you can use Verilator to write your tests. In my case, I am very comfortable using SystemVerilog to write the tests since I don’t have to change my mind to change the programming language when I am developing the module or the verification.