Increasing ADC resolution using oversampling.

After a few post dedicated exclusively to the FPGA, on this post I going to talk about a technique that can help us to improve the ADC resolution. To study this technique, we will use as a example the ADC which is based the Digilent’s ZMOD ADC, the AD9648.

First of all, we need to know what is exactly the resolution of the ADC. In general, if we want to know the resolution, we only have to check the number of bits of the ADC, and the divide the full scale and the total of binary combinations. We can normalize the resolution by changing the full scale by 1. Being the resolution only a function of the number of bits.

\[ADC_{RES}=\frac{1}{2^n}\]

This resolution, is the maximal theoretical resolution of the ADC converter itself, that is, the resolution that ADC can achieve with a clean signal. In the real world, clean signals are like a unicorns, so we never can talk about clean signals in a real development. There are waste that will be added to the signal, and the ability of the ADC to discard that waste in favor of the real signal we want to acquire, is what make an ADC have a better or worst resolution. This is easy to understand if we think in a 4 bit ADC, with a full scale of 1V. This ADC has 16 binary combinations to translate a signal, that is, the ADC will increment one binary step every 0.0625 voltage steps at the input. If the ADC has an input white noise of 0.07 volts, we never could know the real value of the LSB, because the level of noise is greater than the theoretical resolution, so the real resolution will be decreased in 1 bit. Notice that this is a simple explanation of the problem, but in essence this is very close to the reality.

For this case, we will assume that the input noise on the ADC is less than LSB. Even in this case, we will have an error due to changes less than step value won’t be acquired, This error is named quantification noise, and the ability of the ADC to discard this noise is the Signal-to-noise Ratio. The temporal shape of that error is a sawtooth, and it is explained here, and the equation that describes this error is the next.

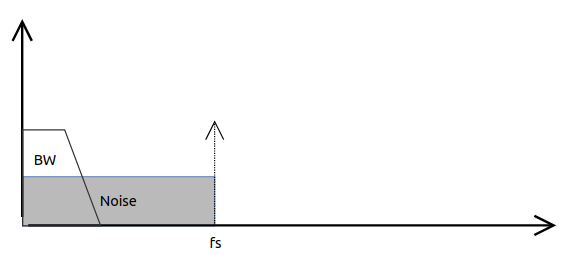
\[SNR=(6.02N)+1.76\]

It is important to notice that this equation describes the signal-to-noise ratio between 0 and the Nyquist frequency, and here comes the magic. If we have an acquisition system with an interest bandwidth that corresponds exactly to the Nyquist frequency, the shape of the noise in the frecuency domain looks like:

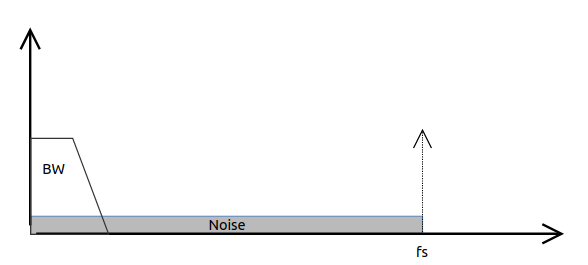
Our signal-to-noise ratio will be the worst as possible, because all the noise is located on our interest band. Even if we apply a digital filtering, we only will discard the half of the noise. To improve that, we need to apply a technique named oversampling, that is increase the acquisition frequency, to reduce the noise on the interest bandwidth. The effect is shown on the next image.

As we can see, the noise is distributed along the new acquisition bandwidth, making the interest bandwidth cleaner. This is translated in a SNR increase. The new increased SNR looks like the next.

\[SNR=(6.02N)+1.76+10log_{10}(\frac{fs}{2BW})\]

In this new equation, the sampling frequency is added in a new term named the process gain. Studying the equation, we can notice that an increase in the SNR of 6.02dB, is equivalent to increase the number of bits in 1, due to the first term. So, if we make the process gain equal to 6.02 will be equivalent to increase 1 bit resolution. According the equation, if BW is equal to fs/2, the process gain is 0, but if we multiply by 4 the fs, that is an oversampling ratio of 4, the process gain is equal to 6.02, and if we multiply the fs by 16, the resulting value is 12.04, so we can say that the over sampling ratio (OSR) we have to apply is 4 raised to the number of resolution bits we want to increase.

\[OSR=2^{\delta nBits}\]

To test, I have used a Digilent Eclypse Z7, and the ZMOD ADC, that has a sampling frequency of 100MHZ, with 14 bits of theoretical resolution. I will create an square signal and test the algorithm on the steady part of the signal. The module will perform a decimation, and every 4 samples at the input of 14 bits, module will compute 1 sample of 15 bits.

/**
  Module name: decimate_x4_v1_0
  Author: P Trujillo ([email protected])
  Date: Nov 2020
  Description: Module to decimate by 4 increasing 1 bit resolution.
  Revision: 1.0 Module created.
**/

module decimate_x4_v1_0 #(
  parameter pw_input_width = 14
  )(
  input clk,
  input rstn,
  input signed [pw_input_width-1:0] i_data,
  input i_data_valid,

  output o_data_valid,
  output reg signed [pw_input_width:0] or_data
  );

  reg signed [pw_input_width:0] rp_data_0;
  reg signed [pw_input_width:0] rp_data_1;
  reg signed [pw_input_width:0] rp_data_2;
  reg signed [pw_input_width:0] rp_data_3;

  reg [1:0] r2_data_counter;

  always @(posedge clk)
    if (!rstn) begin
      rp_data_1 <= 0;
      rp_data_2 <= 0;
      rp_data_3 <= 0;
      r2_data_counter <= 2'd0;
    end
    else
      if (i_data_valid) begin
        rp_data_0 <= {i_data[13], i_data};
        rp_data_1 <= rp_data_0;
        rp_data_2 <= rp_data_1;
        rp_data_3 <= rp_data_2;

        r2_data_counter <= r2_data_counter + 2'b1;
      end

  always @(posedge clk)
    if (!rstn)
      or_data <= 0;
    else
      if (&r2_data_counter)
        or_data <= rp_data_0[14:1] + rp_data_1[14:1] + rp_data_2[14:1] + rp_data_3[14:1];

endmodule

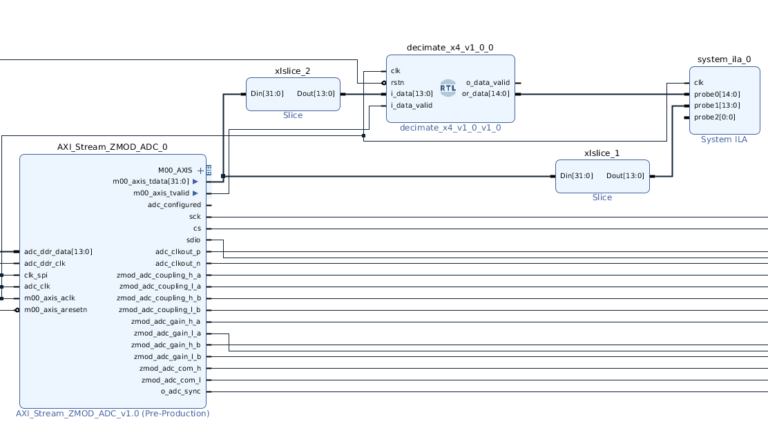
The block design looks like the next:

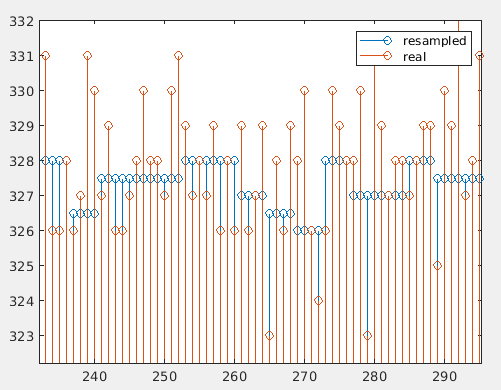
The result of this test can be checked on the next diagram, where the red dot represents the acquired signal, and the blue dots are corresponding with the resampled signal. We can see if, we scale both with the same factor, the blue signal can has a resolution of 0.5, however, the red signal is moving over the integer values.

Now, the question is, may I acquire a dynamic signal with this method to improve my ADC resolution? The answer is it depends. This method is based on take 4 samples where before only 1 samples was taken, and this has a limitation. The extra bit comes from the discarding the noise of the signal, but if is the interest signal the reason of the signal variation, this method is not valid, because we would be discarding the signal of interest. Despite this, if the sampling frequency is higher than the interest signal variation, in other words, the variation if the signal in the sampling period is low, we can use this method without problem.