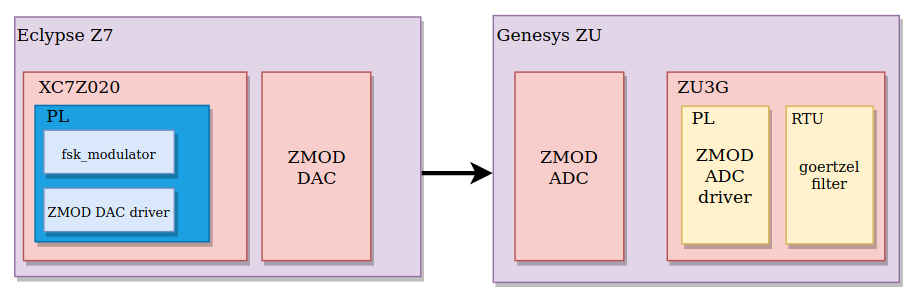
Single tone detector with Genesys ZU and RTU.

When I started to investigate about signal processing, what made me feel happier was decode a signal that, apparently, has no sense. Discrete Fourier Transform (DFT) turns something meaningless into something meaningful. That is amazing but, if we are looking for the value of one component of the signal, compute the entire DFT can be like use a sledgehammer to crack a nut. Luckily, Gerald Goertzel made some modifications on the DFT algorithm to make it easier to compute. Goertzel algorithm is optimized to compute low number of harmonics because, if we want to compute a high amount of them, there are more efficient methods like Cooley-Tukey.

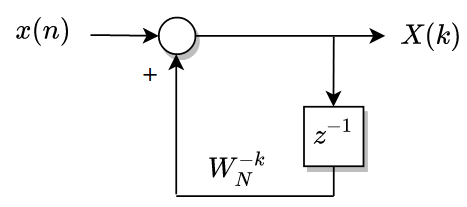
First, we have to study the DFT equation, and notice that, for only one harmonic, the operation turns recursive.

\[x[0]+W_{N}^{k}(x[1]+W_{N}^{k}(x[2]+W_{N}^{k}(x[3]+W_{N}^{k}(x[4]...)))\]

The above equation, we can be drawn as follows

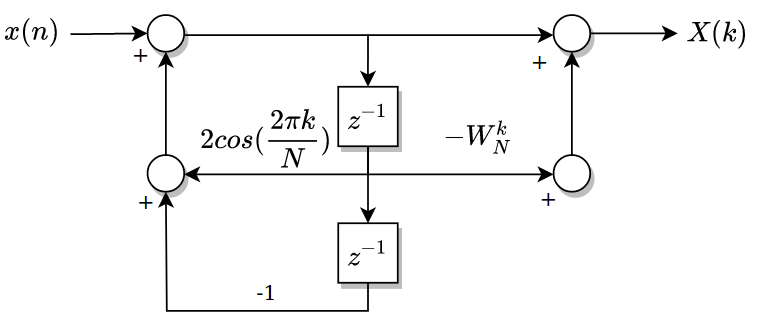
Term \(W\) is a complex term, so for each sample, 4 real operations and 4 imaginary operations has to be computed. This is translated in a biggest delay. For the equation of the above H(s) system, we can multiply numerator and denominator by the same value, and the result of the equation is as follows.

\[H(z)=\frac{1}{1-W_N^{-k}} \cdot \frac{1-W_N^{-k}z^{-1}}{1-W_N^{-k}z^{-1}}=\frac{1-W_N^{-k}z^{-1}}{1-2cos(2 \pi k/N)z^{-1}+z^{-2}}\]

This system can be executed as a second order filter with only 4 multiplications for each sample.

To test the Goertzel algorithm, I will use the new Genesys ZU board. This development board is based on Zynq UltraScale, so we have inside the device, an RTU running up to 600MHz, and is here where the Goertzel filter will be executed. Signal we will process with the algorithm will be generated by the Eclypse Z7 Board, and the module I have developed, generates a Frequency Shift Modulation (FSK), where there is a 3MHz signal, for logic ‘0’, and 30MHz signal for the logic ‘1’.

Code on the Eclypse Z7 is developed all in the PL, that allows me to achieve high response speed. Generator code is based on a FSK modulator which reads a sinusoidal signal from BRAM. Signal has 32 points, and the read index is increased by 1 every clock event. When I want to transmit a ‘1’, the index is increased by 10, so the output frequency is multiplied by 10. This method decreases the resolution of the signal but the harmonic spectrum keeps clean, so the Goertzel filter can detect the corresponding harmonic without problems.

Signal generated by the FSK modulator is synthesized by the ZMOD DAC through the ZMOD DAC driver, and transmitted to the Genesys ZU Board.

Code on Genesys ZU board is running part on the PL and part on the RTU. In the PL I have developed the ZMOD ADC driver. In this case, since Zynq US+ is not a part of the 7 series of Xilinx, there are differences in the primitives, and the IDDR of the 7 series is not in the Ultrascale Architecture, instead of that, we have IDDRE2, which is very similar, but needs 2 clocks, one of them inverted. This inversion can be done out of the primitive, so both parameters IS_C_INVERTED and IS_CB_INVERTED have to be configured as 0, or we can use the same clock signal (BUFG is needed), and indicate it to the primitive to do the inversion inside, and that’s the configuration I have used.

IDDRE1 #(
.DDR_CLK_EDGE("SAME_EDGE"),
.IS_CB_INVERTED(1'b1),
.IS_C_INVERTED(1'b0)
)
IDDRE1_inst (
.Q1(o14_data_a[i]),
.Q2(o14_data_b[i]),
.C(i_dco),
.CB(i_dco),
.D(i14_data[i]),
.R(!rstn)
);

The rest of the code, including clock forwarding, is similar to the used one in the Eclypse Z7.

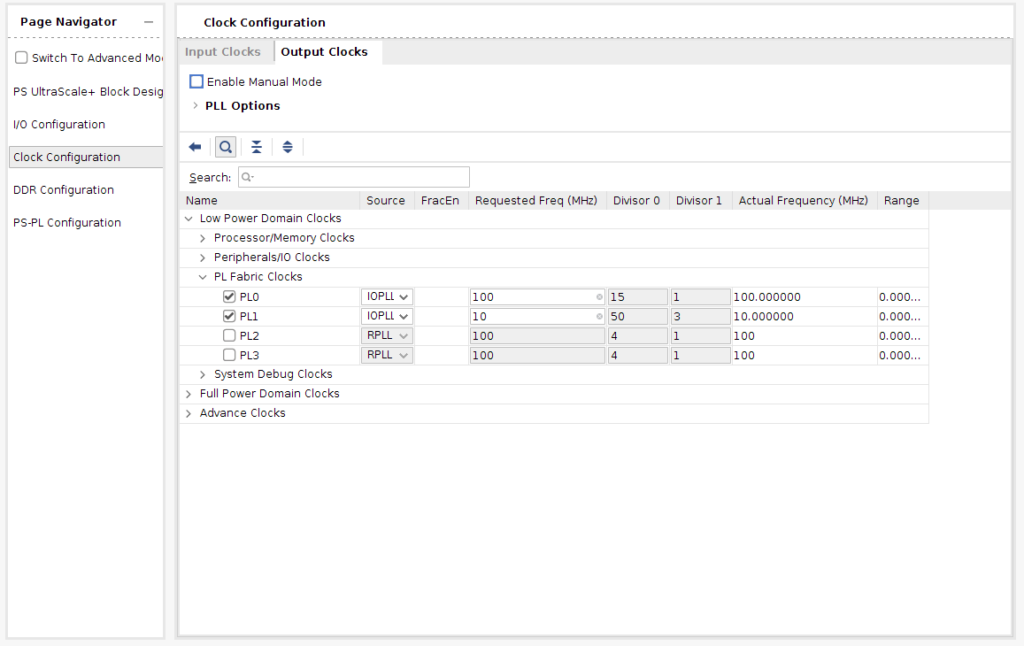
Clocks for the design are generated by the PS, and we will need one of 100MHz for the signal processing system, and one of 50MHz for the SPI communication with the ADC. In Ultrascale architecture, we have different power domains, mainly Low Power Domain and Full Power Domain. Also we have the Battery Power Domain, but we do not use it for now. Each power domain supplies different parts inside the device, including clocks. To enable the PL fabric clocks, we have to enable the Low Power Domain, and the corresponding PL fabric clocks.

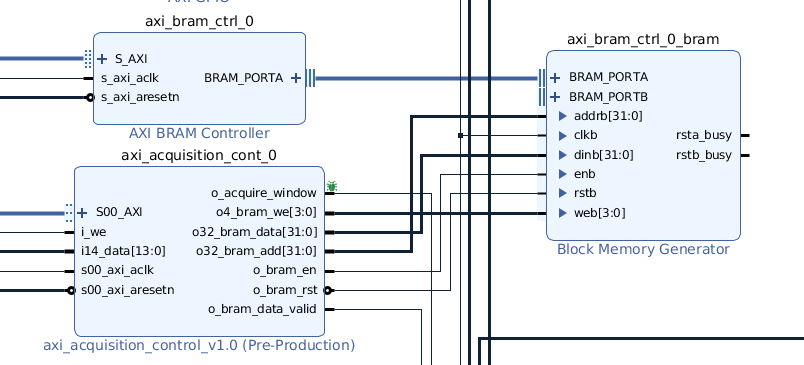
Data from the ZMOD ADC driver will be stored in BRAM by the acquisition control module. This module will write the number of samples configured by AXI in a BRAM configured as True Dual Port RAM. The other port will be connected to a BRAM AXI Controller, so data on BRAM can be wrote and read by PL and PS. To me, this is the easiest way to share medium amount of data between PL and PS.

Once the block design is complete, Generate bitstream, Export Hardware and Launch SDK.

Inside SDK, we have to create a BSP for the RTU0, without any specific library. Once generated, we will create a project, and a new C source.

In the source, first we have to define the constants used in Goertzel filter and create the pointer to data

long* x;

x = (long*)0x80000000

/* Goertzel constant definition */
w_re10 = cos(2*pi*10/n_samples);
w_im10 = sin(2*pi*10/n_samples);
c10 = 2*cos(2*pi*10/n_samples);

Then, in a for loop we will execute the algorithm for all samples.

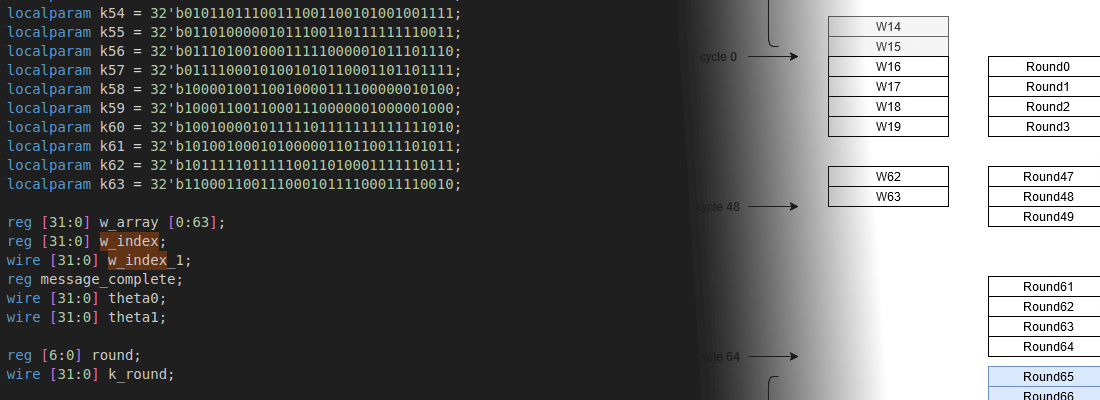
for (i=0; i<(n_samples*4); i=i+4) {
    y_re10 = (float)*x*w_re10-x_1+c10*y_re10_1-y_re10_2;
    y_im10 = (float)*x*w_im10+c10*y_im10_1-y_im10_2;

    y_re10_2 = y_re10_1;
    y_re10_1 = y_re10;
    y_im10_2 = y_im10_1;
    y_im10_1 = y_im10; 

    x_1 = *x;
    x++; /* New sample */
}

At the end of the loop, value on y_re10 and y_im10 will be the real and imaginary values of the 10th harmonic, and we can distinguish if the read signal has the 10th harmonic or not, comparing the absolute value of both with a threshold.

The Goertzel algorithm works fine on Zynq Ultrascale thanks to the RTU, but the algorithm has a problem of using it as a signal processing at the edge because it needs to acquire an entire window for execute it. Also, even the RTU runs up to 600MHz, 500MHz in my case because the speed grade, the processing of all samples takes 60us, so the maximum that we can process is 16kHz.

Also, with this algorithm we can not estimate the final result with a less number of samples, so we need to wait up to all samples are processed to know the final result.

For improve that we have several options, most of all with the power of the Zynq US+. First we can execute the algorithm on the PL, so we can process each signal at the same time that is acquired. To do that, we need a clock at least twice of the sampling clock, but this is not a problem because the PLL from PS to PL can achieve up to 533MHz, and as the PL of the device is big enough, we will not have timing problems.

Also we can change the algorithm to a Notch Filter + Peak Detector. With this method, if the harmonic that we are looking for is the 10th, depending on the Q factor of the filter, we can obtain a correct signal in 2 or 3 cycles, at this moment the peak of the signal will be increased, so we can detect the value of this harmonic at 2/10 or 3/10 of the Goertzel time. Notice that with this method, we do not have information of the signal phase.

Other option is use twice of power. Zynq US+ devices has a dual core RTU that can run in Split mode. Unlike DFT where we can implement a Decimation In Time, on IIR filters we can’t do that because we need the past outputs to compute the next, but we can acquire windows at twice of frequency. In this case we will keep the delay of 60us, but we will improve the throughput, because the output will be updated at twice of the frequency.

Regarding the acquisition, SYZYGY and ADC ZMOD allow us to achieve high frequencies, so I think I can achieve best performance with Genesys ZU.

Thanks for read!